视频

了解更多
在我看来,这篇文章是关于世界上最激动人心的两件事:概率数据结构和 Redis 模块。 如果您听说过其中一种,您肯定能理解我的热情,但如果您想了解地球上最酷的东西,请继续阅读。
我将从以下声明开始:大规模低延迟数据处理具有挑战性。 所涉及的数据量和速度会使实时分析变得非常困难。 由于其高性能和多功能性,Redis 通常用于解决此类挑战。 它能够以亚毫秒级的延迟存储、操作和服务多种形式的数据,使其成为许多需要在线计算的理想数据容器。
但一切都是相对的,并且存在如此极端的规模,以至于准确的实时分析在实践中是不可能的。 复杂的问题只会随着规模的扩大而变得更加困难,但我们往往忘记了简单的问题也遵循同样的规则。 即使像求和这样的基本操作,一旦数据太大、太快,或者我们没有足够的资源来处理它,也会变成一项艰巨的任务。 虽然资源总是有限且昂贵的,但数据却像没有人管一样不断增长。
Count-min sketch(也称为 CM sketch)是一种概率数据结构,一旦您掌握了它的工作原理,更重要的是,如何使用它,它就非常有用。
幸运的是,CM sketch 的简单特性使新手相对容易理解(事实证明,我的许多朋友都无法理解这篇Top-K 博客)。
CM sketch 已经成为 Redis 模块好几年了,最近被重写为 RedisBloom 模块 v2.0 的一部分。 但在我们深入研究 CM sketch 之前,重要的是要理解为什么您要使用任何概率数据结构。 在速度、空间和准确性的三角形中,概率数据结构牺牲了一些准确性以获得空间——可能很多空间! 对速度的影响因算法和集合大小而异。
正确的概率数据结构允许您仅保留数据集中部分信息,以换取准确性的降低。 当然,在许多情况下(例如银行帐户),降低准确性是不可接受的。 但对于推荐电影或向网站用户展示广告而言,相对罕见的错误的代价很低,而且节省的空间可能相当大。
基本上,CM sketch 的工作原理是将数据集中所有项目的计数聚合到多个计数器数组中。 在查询时,它返回所有数组中项目的最小计数,这有望最大限度地减少由冲突引起的计数膨胀。 出现率或分数较低的项目(“鼠标流”)的计数低于错误率,因此您会丢失有关其真实计数的任何数据,并且它们被视为噪声。 对于出现率或分数较高的项目(“大象流”),只需使用收到的计数即可。 考虑到 CM sketch 的大小是恒定的,并且它可以用于无限数量的项目,您可以看到在存储空间中节省的巨大潜力。
作为背景,草图是一类数据结构及其随附的算法。 它们捕获数据的性质,以便在利用恒定或亚线性空间的同时回答有关数据的问题。 CM sketch 由 Graham Cormode 和 S. Muthu Muthukrishnan 在 2005 年发表的一篇名为“改进的数据流概要:Count-Min Sketch 及其应用”的论文中描述。
CM sketch 使用多个计数器数组来支持其主要用例。 我们将数组的数量称为“深度”,并将每个数组中的计数器数量称为“宽度”。
每当我们收到一个项目时,我们使用一个哈希函数(它将一个元素——一个单词、句子、数字或二进制——转换为一个数字,该数字可用作集合/数组中的位置或作为指纹)来计算项目的位置并增加每个数组的计数器。 每个关联的计数器的值等于或高于项目的实际值。 当我们进行查询时,我们使用相同的哈希函数遍历所有数组,并获取与我们的项目关联的计数器。 然后,我们返回遇到的最小值,因为我们知道我们的值被夸大了(或相等)。
即使我们知道许多项目会导致大多数计数器增加,但由于自然冲突(当不同的项目收到相同的位置时),我们接受“噪声”,只要它保持在我们期望的错误率范围内。
数学公式表明,当深度为 10,宽度为 2,000 时,没有错误的概率为 99.9%,错误率为 0.1%。 (这是总增量的百分比,而不是唯一项目的百分比)。
在实际数字中,这意味着如果您添加 100 万个唯一项目,平均而言,每个项目将收到 500 的值 (1M/2K)。 虽然这看起来不成比例,但这完全在我们 0.1% 的错误率范围内,即 100 万个项目中 1,000 个。
同样,如果 10 只大象每次出现 10,000 次,它们在所有集合中的值将为 10,000 或更多。 每当我们将来计算它们时,我们会看到一只大象在我们面前。 对于所有其他数字(即,所有实际计数为 1 的老鼠),它们不太可能与所有集合中的大象发生冲突(因为 CM sketch 仅考虑最小计数),因为这种情况发生的概率很小,如果您增加初始化 CM sketch 时的深度,则概率会进一步降低。
现在我们了解了 CM sketch 的行为,我们能用这个小野兽做什么? 以下是一些常见的用例
在 RedisBloom 中,CM sketch 的 API 简单易用
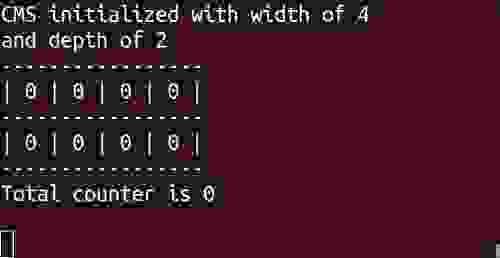
以下命令用于创建此帖子顶部的动画示例

如您所见,“Redis”的值为 4 而不是 3。 这种行为是预期的,因为在 CM sketch 中,项目的计数很可能会膨胀。
软件工程的核心在于权衡取舍。为了以具有成本效益的方式应对这些挑战,一种流行的做法是牺牲准确性以换取效率。Redis 实现的 HyperLogLog 就是这种做法的典范。HyperLogLog 是一种数据结构,旨在高效地回答关于集合基数的查询。HyperLogLog 属于一类被称为“草图”的数据结构,就像现实世界中的艺术作品一样,它们通过近似来传达信息。
概括地说,草图是数据结构(及其配套算法),它捕获数据的本质——回答关于数据的问题,而无需实际存储数据本身。正式地说,草图很有用,因为它们具有亚线性渐近计算复杂度,因此需要更少的计算能力和/或存储空间。但是,没有免费的午餐,效率的提高会被答案的准确性所抵消。然而,在许多情况下,只要误差能控制在阈值以下,就是可以接受的。一个好的数据草图会欣然承认它的误差,事实上,许多草图都会参数化它们的误差(或所述误差的概率),以便可以由用户定义。
好的草图是高效的,并且具有误差概率的上限,但优秀的草图是可以并行计算的。可并行化的草图可以在数据的各个部分上独立准备,并允许将其各个部分组合成有意义且一致的聚合。因为一个优秀的草图的每个部分都可以在不同的位置和/或时间计算,所以并行性使得应用直接的分而治之方法来解决扩展挑战成为可能。
前面提到的 HyperLogLog 是一种优秀的草图,但它只适用于回答特定类型的问题。另一个非常有价值的工具是 Count Min Sketch (CMS),如 G. Cormode 和 S. Muthukrishnan 的论文 “一种改进的数据流摘要:Count-Min Sketch 及其应用” 中所述。这种巧妙的装置被设计用来提供关于样本频率的答案,这是很大一部分分析过程中常见的构建块。
如果有足够的时间和资源,计算样本的频率是一个简单的过程——只需保持对每个样本(看到的东西)的观察次数(看到次数)的计数,然后将其除以观察总数,即可获得该样本的频率。但是,在高规模、低延迟数据处理的背景下,时间或资源永远都不够。无论数据规模如何,都必须在数据流入时立即提供答案,并且抽样空间的庞大规模使得为每个样本保留计数器变得不可行。
因此,与其准确地跟踪每个样本,不如尝试估计频率。一种方法是随机抽样观察结果,并希望该样本通常反映整体的属性。这种方法的问题在于,确保真正的随机性是一项困难的任务,因此随机抽样的成功可能会受到我们的选择过程和/或数据本身属性的限制。这就是 CMS 的用武之地,它采用了一种截然不同的方法,乍一看,它似乎与优秀的草图相反:CMS 不仅记录每个观察结果,而且每个观察结果都记录在多个计数器中!
当然,这里有一个巧妙的转折,它既聪明又简单。原始论文(及其更轻量级的版本 “使用 Count-Min 数据结构近似数据”)很好地解释了这一点,但我仍然会尝试总结一下。CMS 的聪明之处在于它存储样本的方式:它不单独跟踪每个唯一样本,而是使用其哈希值。样本的哈希值用作固定大小(在论文中参数化为 d)的计数器数组的索引。通过使用几个(参数 w)不同的哈希函数及其各自的数组,草图通过选择样本的所有相关计数器中的最小值来处理在查询结构时发现的哈希冲突。
我们需要一个例子,所以让我们做一个简单的草图来说明数据结构的内部工作原理。为了保持草图的简单,我们将使用较小的参数值。我们将 w 设置为 3,这意味着我们将使用三个哈希函数——分别表示为 h1、h2 和 h3,并将 d 设置为 4。为了存储草图的计数器,我们将使用一个 3×4 的数组,总共有 12 个元素,初始化为 0。
现在我们可以检查将样本添加到草图中会发生什么。假设样本一个接一个地到达,并且第一个样本(表示为 s1)的哈希值为:h1(s1) = 1,h2(s1) = 2 和 h3(s1) = 3。为了在草图中记录 s1,我们将每个哈希函数的计数器在相关索引处递增 1。下表显示了数组的初始状态和当前状态

尽管草图中只有一个样本,但我们已经可以有效地查询它。请记住,样本的观察次数是其所有计数器的最小值,因此 s1 的观察次数可以通过以下方式获得:
min(array[1][h1(s1)], array[2][h2(s1)], array[3][h3(s1)]) = 草图还可以回答关于尚未添加的样本的查询。假设 h1(s2) = 4, h2(s2) = 4, h3(s2) = 4,请注意,查询 s2 将返回结果 0。让我们继续将 s2 和 s3 (h1(s3) = 1, h2(s3) = 1, h3(s3) = 1) 添加到草图中,产生以下结果
min(array[1][1], array[2][2], array[3][3]) =
min(1,1,1) = 1

在我们人为设计的例子中,几乎所有样本的哈希都映射到唯一的计数器,唯一的例外是 h1(s1) 和 h1(s3) 的冲突。因为两个哈希值相同,所以 h1 的第一个计数器现在的值为 2。由于草图选择所有计数器的最小值,因此对 s1 和 s3 的查询仍然返回正确的结果 1。然而,最终,一旦发生足够的冲突,查询的结果将变得不那么准确。
CMS 的两个参数——w 和 d——决定了它的空间/时间要求,以及它的误差概率和最大值。初始化草图的一种更直观的方法是提供误差的概率和上限,然后允许它导出 w 和 d 所需的值。并行化是可能的,因为任意数量的子草图可以简单地合并为数组之和,只要在构造它们时使用相同的参数和哈希函数。
可以通过查看其需求来证明 Count Min Sketch 的效率。CMS 的空间复杂度是 w、d 和它使用的计数器的宽度的乘积。例如,使用 10 个哈希函数和 2000 个计数器的数组创建的误差率为 0.01%,概率为 0.01% 的草图。假设使用 16 位计数器,则生成的草图的数据结构的总体内存需求为 40KB(需要几个额外的字节来存储观察总数和一些指针)。草图的另一个计算方面同样令人满意——因为哈希函数的生成和计算都很便宜,所以访问数据结构(无论是读取还是写入)也以恒定时间执行。
CMS 还有更多内容;草图的作者还展示了它如何用于回答其他类似的问题。这些包括估计百分位数和识别重击者(频繁项目),但这超出了本文的范围。
CMS 肯定是一个优秀的草图,但至少有两件事阻止它达到完美。我对 CMS 的第一个保留意见是它可能有偏差,因此高估了观察次数较少的样本的频率。CMS 的偏差是众所周知的,并且已经提出了几项改进建议。最新的是 Count Min Log Sketch (“使用近似计数器进行近似计数” 来自 G. Pitel 和 G. Fouquier),它本质上用对数寄存器替换 CMS 的线性寄存器,以减少相对误差,并允许更高的计数,而无需增加计数器寄存器的宽度。
虽然上述保留意见是每个人都认同的(尽管只有那些理解数据结构的人),但我对 Redis 社区的第二个保留意见是独有的。为了解释,我必须介绍 Redis Modules。
Redis Modules 早在今年就由 antirez 在 RedisConf 上发布,它彻底颠覆了我们的世界。模块是可以动态加载到服务器上的动态链接库,它允许 Redis 用户比 Redis 本身移动得更快,并到达以前从未梦想过的地方。虽然这篇文章不是介绍模块是什么或如何制作它们,但 这篇文章是(以及 这篇文章,以及 这个网络研讨会)。
除了它的极端实用性之外,我想编写 Count Min Sketch Redis 模块的原因有很多。一部分是学习经验,一部分是对模块 API 的评估,但主要是将新的数据结构建模到 Redis 中非常有趣。该模块为 Redis 提供了一个接口,用于向草图添加观察结果、查询草图以及将多个草图合并为一个。
该模块将草图的数据存储在 Redis String 中,并使用直接内存访问 (DMA) 将键的内容映射到其内部数据结构。我还没有对它进行详尽的性能基准测试,但我从本地测试中得到的初步印象是它的性能与任何核心 Redis 命令一样好。像我们的其他模块一样,countminsketch 是开源的,我鼓励您尝试并对其进行修改。
在签署之前,我想信守承诺并分享我对 CMS 特有的 Redis 保留意见。该问题也适用于其他草图和数据结构,即 CMS 需要在使用前进行设置/初始化/创建。需要强制初始化阶段(例如 CMS 参数设置)会打破 Redis 的基本模式之一——数据结构不需要在使用前显式声明,因为它们可以按需创建。为了使模块看起来更像 Redis 并解决这种反模式,该模块在使用默认参数值时,当隐式暗示新的草图时(例如,在不存在的键上使用 CMS.ADD 命令),但也允许使用给定的参数创建新的空草图。
概率数据结构或草图是强大的工具,使我们能够以高效且足够准确的方式跟上大数据增长和延迟预算缩减的步伐。本文中提到的两个草图,以及其他草图(例如 Bloom Filter 和 T-digest)正迅速成为现代数据处理人员武器库中不可或缺的工具。模块允许您使用以本机速度运行并具有本地数据访问权限的自定义数据类型和命令来扩展 Redis。可能性是无限的,没有什么是不可能的。
想了解更多关于 Redis 模块以及如何开发它们的信息吗?是否有您想讨论或添加到 Redis 中的数据结构,无论是否是概率性的?欢迎通过我的 Twitter 账号或通过电子邮件联系我,讨论任何事情 – 我非常乐意提供帮助 🙂