本文是介绍 Redis-ML 模块系列文章的第二部分。
在该系列文章的上一篇文章中,我们使用 Python 的 scikit-learn 包和 Redis 构建了一个预测波士顿地区房屋中位价的系统。使用线性回归(一种强大的统计工具),我们构建了一个定价模型,该模型使用房屋平均房间数量预测社区的房屋中位价。
在文章结尾,我们提到下一篇文章将介绍分类,这是一个根据先前同类项目示例识别某物所属类别的机器学习过程。但与其过早地转向该主题,本文将补充一些关于线性回归的未尽事宜。
本文中的示例代码需要与上一篇文章中的代码相同的 Redis 模块和 Python 包。如果您已经搭建好环境,可以跳过技术要求部分。任何其他要求将在介绍示例代码时予以说明。
Redis 要求
本文中的示例代码需要 Redis 4.0 或更高版本,并加载了Redis-ML模块。要运行本文中的示例,请启动 Redis 并使用 loadmodule 指令加载 Redis-ML 模块。
redis-server --loadmodule /path/to/redis-ml/module.so
您可以通过从 Redis 命令行界面(redis-cli)运行 MODULE LIST 命令来验证 Redis-ML 模块是否已加载,并确保 redis-ml 出现在已加载模块列表中:
127.0.0.1:6379> MODULE list 1) "name" 2) "redis-ml" 3) "ver" 4) (integer) 1
或者,您可以运行由Shay Nativ提供的 Redis-ML Docker 容器,该容器预配置了您所需的依赖项。要在本地部署 redis-ml 容器,请使用以下命令启动它:
docker run -it -p 6379:6379 shaynativ/redis-ml
Docker run 命令会在需要时自动下载容器并启动一个监听端口 6379 的 Redis 4.0 服务器。-p 选项将主机上的端口 6379 映射到容器中的端口 6379,因此请为您的环境采取适当的安全预防措施。
本文中的示例代码与第一部分中的示例代码具有相同的 Redis 要求,因此如果您已经搭建好环境以试验该文章中的代码,则可以继续将其用于本文及后续文章。
Python 要求
要运行本文中的 Python 示例代码,您需要安装以下包
您可以使用 pip3 或您偏好的包管理器安装所有这些包。
线性回归模型
线性回归将两个变量之间的关系表示为一条直线,其标准方程为 y=b + ax。直线的参数(斜率和截距)因数据集而异,但模型的结构是相同的。
任何能够对数据集执行线性回归以发现直线参数的工具包都可以与 Redis 结合使用。为了说明模型的独立性,我们将使用 R(一种用于数据分析和实验的统计语言和环境)重建我们的房屋价格预测器。R 提供了各种数据分析功能,包括用于执行线性回归的包。R 通常用作交互式数据探索工具,而不是批处理系统。
以下代码在 mac OS 上使用 R.app 的 3.4.1 版本进行了测试。如果您有兴趣运行代码,可以从R Project 网站下载该环境。代码依赖于MASS包;如果您的 R 版本不包含MASS包,请使用 R 的内置包管理器下载它。
上一篇文章中构建的房屋价格预测器使用 Python 和 scikit-learn 包对样本数据运行线性回归。一旦线性回归过程找到了最能代表房间数量与社区房屋中位价之间关系的直线,我们就在 Redis 中重新创建了这条直线,并使用 Redis 根据观测到的特征预测未知房屋价格。
在本文中,我们将通过在 R 中重新实现我们的线性回归程序来演示如何将不同的工具包与 Redis 结合使用。以下 R 代码将复制上一篇文章中我们的 Python 代码执行的线性回归
# load our data library(MASS) boston.data <- MASS::Boston # split the dataframe into train and test data sets boston.train <- boston.data[1:400, ] boston.test <- boston.data[401:506, ] # fit a linear regression using the rm column to our data boston.lm = lm(medv ~ rm, data=boston.train) # display model parameters summary(boston.lm)
即使您之前从未接触过 R,代码也应该很容易理解。程序的第一部分加载我们的数据。波士顿房屋数据集是机器学习教学中使用的经典数据集。R,像许多统计工具包一样,包含几个经典数据集。对于 R 来说,波士顿房屋数据集包含在MASS包中,因此在访问数据之前,我们必须加载MASS包。
代码的第二部分将房屋数据分成训练集和测试集。按照 Python 版本中使用的方法,我们从前 400 个数据点创建训练集,并将剩余的 106 个数据点保留用于测试集。由于 R 将我们的数据存储为数据框(data frame)而不是数组(scikit 这样做),我们可以跳过我们在 Python 中执行的切片和列提取操作,这些操作使我们的房间数据列更容易访问。
线性回归在 R 中使用内置的线性回归函数(lm)执行。
lm 的第一个参数用于描述数据框中的预测变量和预测值。对于这个问题,我们使用medv ~ rm,因为我们正在根据平均房间数数据预测房屋中位价数据。
在脚本的最后一步,summary 方法用于向用户显示拟合直线的系数。
绘制我们的结果并与之前的代码结果进行比较
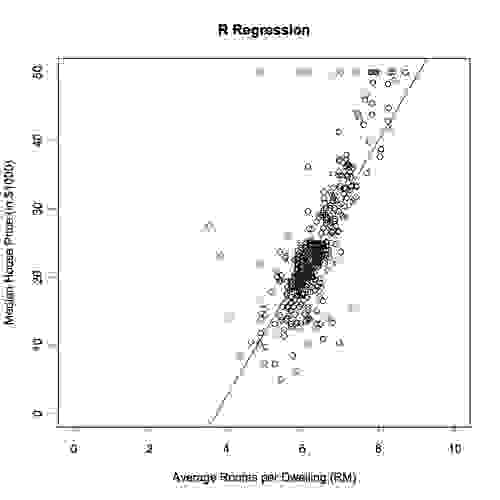
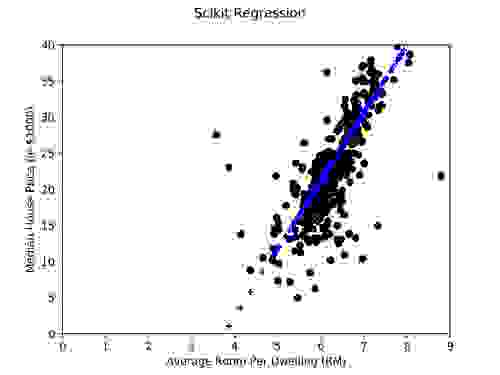
summary 方法显示线性回归过程确定的系数为:
Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -35.2609 2.6289 -13.41 <2e-16 *** rm 9.4055 0.4121 22.82 <2e-16 ***
与 scikit-learn 包一样,R 确定直线的斜率为 9.4055,截距为 -35.2609。我们的 R 代码与 scikit 的结果完全相同,精确到小数点后第四位。
从这一点开始,设置 Redis 以预测房屋价格的步骤与之前相同。首先,使用ML.LINREG.SET命令创建一个线性回归键:
127.0.0.1:6379> ML.LINREG.SET boston_house_price:rm-only -35.2609 9.4055
OK
创建键后,使用ML.LINREG.PREDICT命令预测房屋价值:
127.0.0.1:6379> ML.LINREG.PREDICT boston_house_price:rm-only 6.2 "23.053200000000004”
将结果四舍五入到小数点后四位后,我们仍然得到该特定社区的房屋中位价估计值为 23,053 美元(请记住,我们的房价是以千美元为单位的)。
这可能是您第一次也是唯一一次运行 R,但重要的是要记住,在使用 Redis 服务模型时,模型(而不是工具包)才是最重要的。
我们在上一篇文章中没有涵盖的线性回归的另一个重要主题是多元线性回归。
多元线性回归
到目前为止,在所有示例中,我们都使用了单个变量来预测一个值。我们的房屋预测器仅使用平均房间大小来预测房屋中位值,但数据集中有与特定房屋中位价关联的多个数据值(称为“特征”)。
线性回归通常使用多个变量来预测一个值。这给我们一个看起来像y=0+1x1+ … + nxn 的模型。在多元线性回归中,我们需要求解截距和每个变量的系数。
以下代码实现了多元线性回归,尝试使用我们的波士顿房屋数据中的所有可用数据列来拟合预测直线
import redis from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression # load out data boston = load_boston() # slice the data into train and test sets x_train = boston.data[:400] x_test = boston.data[400:] y_train = boston.target[:400,] y_test = boston.target[400:,] # fit the regression line lm = LinearRegression() lm.fit(x_train, y_train) y_predict = lm.predict(x_test) coef = lm.coef_ inter = lm.intercept_ for col, c in zip(boston.feature_names, coef): print('{colname:7}:t{coef:0.6f}'.format(colname=col,coef=c)) print("Intercept: {inter}".format(inter=inter)) # set the linear regression in Redis cmd = ["ML.LINREG.SET", "boston_house_price:full"] cmd.append(str(inter)) cmd.extend([str(c) for c in coef]) r = redis.StrictRedis('localhost', 6379) r.execute_command(*cmd)
下表显示了 scikit 确定的最佳预测直线的系数。每个系数对应一个特定变量(特征)。例如,在我们的多元线性回归中,平均房间数的常数现在是 4.887730,而不是仅考虑房间数据时得到的 9.4055。
CRIM : -0.191246 ZN : 0.044229 INDUS : 0.055221 CHAS : 1.716314 NOX : -14.995722 RM : 4.887730 AGE : 0.002609 DIS : -1.294808 RAD : 0.484787 TAX : -0.015401 PTRATIO: -0.808795 B : -0.001292 LSTAT : -0.517954 Intercept: 28.672599590856002
然后,我们创建一个 Redis 键boston_house_price:full来存储我们表示的多元线性回归。请记住,Redis 不使用命名参数作为ML.LINREG命令的参数。ML.LINREG.SET 中系数的顺序必须与ML.LINREG.PREDICT 调用中变量值的顺序匹配。例如,使用上面的线性回归代码,我们需要按照以下参数顺序调用我们的ML.LINREG.PREDICT:
127.0.0.1:6379> ML.LINREG.PREDICT boston_house_price:all <CRIM> <ZN> <INDUS> <CHAS> <NOX> <RM> <AGE> <DIS> <RAD> <TAX> <PTRATIO> <B> <LSTAT>
本文演示了工具包的独立性,并解释了多元线性回归,补充了我们关于线性回归的第一篇文章。我们回顾了我们的房屋价格预测器,并使用 R 而不是 Python“重建”它来实现线性回归阶段。
R 将与 scikit 相同的数学模型应用于房屋问题,并学习到相同的直线参数。然后,在 Redis 中设置键并将 Redis 部署为预测系统的过程几乎相同。
在下一篇文章中,我们将探讨逻辑回归以及如何使用 Redis 构建强大的分类引擎。我们保证做到。在此期间,如果您对此文或之前的文章有任何疑问,请在 Twitter 上联系作者(@tague)。