概率数据结构
概率数据结构
Bloom 过滤器是一种概率数据结构,它提供了一种高效的方法来确定性地验证一个条目 不 在集合中。这使得它在尝试从访问成本高的资源(例如通过网络或磁盘)中搜索项目时特别理想:如果我有一个大型的磁盘数据库,并且想知道键 foo 是否存在其中,我可以先查询 Bloom 过滤器,它能确定地告诉我该键是否可能存在(然后可以继续进行磁盘查找),或者是否 不 存在,在这种情况下,我可以放弃昂贵的磁盘查找,直接向上层堆栈发送否定回复。
虽然可以使用其他数据结构(例如哈希表)来执行此操作,但 Bloom 过滤器也非常有用,因为它们每个元素占用的空间非常小,通常以 位(而不是字节!)为单位计算。存在一定比例的误报(这是可控的),但对于初步测试键是否存在于集合中,它们提供了出色的速度,最重要的是出色的空间效率。
Bloom 过滤器广泛应用于各种场景,例如广告投放(确保用户不会频繁看到同一广告);内容推荐系统(确保推荐内容不会频繁出现);数据库(在访问磁盘上的条目之前快速检查其是否存在),等等。
Bloom 过滤器的工作原理
大多数关于 Bloom 过滤器的文献都使用高度符号化和/或数学化的描述来解释它。如果您像我一样在数学方面感到困难,您可能会发现我的解释更有用。
Bloom 过滤器是一个由许多位组成的数组。当一个元素被“添加”到 Bloom 过滤器时,该元素会被哈希。然后将 bit[hashval % nbits] 设置为 1。这看起来与哈希表中桶的映射方式非常相似。要检查某个项是否存在,会计算其哈希值,然后过滤器会查看相应的位是否已设置。
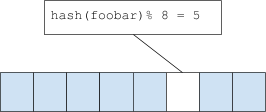
当然,这可能会发生冲突。如果发生冲突,过滤器会返回误报——表明该条目确实已找到(请注意,Bloom 过滤器绝不会返回漏报,也就是说,不会在某个项实际存在时声称它不存在)。
为了降低冲突的风险,一个条目可以使用多个位:该条目会被哈希 bits_per_element (bpe) 次,每次迭代使用不同的种子以产生不同的哈希值,并且对于每个哈希值,相应的 hash % nbits 位都会被设置。要检查一个条目是否存在,待检查的键也会被哈希 bpe 次,如果任何对应的位 未设置,那么就可以确定该项 不 存在。
bpe 的实际值在创建过滤器时确定。一般来说,每个元素的位数越多,误报的可能性就越低。
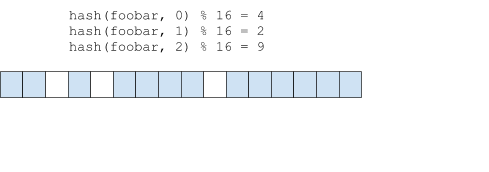
在上面的例子中,所有三个位都需要被设置,过滤器才会返回肯定的结果。
影响 Bloom 过滤器准确性的另一个值是其 填充率,即过滤器中实际设置的位数。如果过滤器中的大多数位都被设置,那么任何特定查找返回“假”的可能性就会降低,从而增加过滤器返回误报的可能性。
可伸缩的 Bloom 过滤器
通常,创建 Bloom 过滤器时必须预先知道它们将包含多少条目。bpe 的数量需要固定,同样,位数组的宽度也是固定的。与哈希表不同,Bloom 过滤器无法“重新平衡”,因为无法知道 哪些 条目是过滤器的一部分(过滤器只能确定给定条目是否 不 存在,但并不实际存储 存在 的条目)。
为了让 Bloom 过滤器能够“伸缩”并容纳比设计容量更多的元素,可以将它们堆叠起来。当一个 Bloom 过滤器达到容量后,会在其之上创建一个新的过滤器。通常,新的过滤器比前一个具有更大的容量,以减少需要再次堆叠过滤器的可能性。
在可堆叠(可伸缩)的 Bloom 过滤器中,检查成员资格现在需要检查每一层是否存在。添加新项现在需要先检查它是否不存在,然后将其添加到当前过滤器中。然而,哈希值仍然只需要计算一次。
创建 Bloom 过滤器时——即使是可伸缩的过滤器,了解它预计包含多少项也非常重要。一个初始层只能包含少量元素的过滤器将显著降低性能,因为它需要更多层才能达到更大的容量。